Hueihuea / 迪杰斯特拉最短路算法的证明

命题1：如果A->B有最短路P 而C属于P 那么A->C的最短路包含于P

易证:假如P中A->C不是最短路 那么一定存在P`使得A->C更短 那么A->C+C->B短于P 这与前提P是A->B的最短路矛盾,故原命题成立。 这其实就是迪杰斯特拉的最优子结构性质。

命题2： 如果P:A->B中所有中间点Mx都满足A->Mx最短 那么P最短

这个命题是错误的，关键在于 缺乏对最后一个中间点到P的距离的考虑。该命题显然不足以支持迪杰斯特拉算法的正确性。

迪杰斯特拉的基本原理：

令起点为O 终点为F 中间顶点记作Pn

维护俩个数组S和U

S代表已经访问的顶点

U代表仍未访问的顶点

每个顶点包含以下属性

-list 记录相邻顶点以及俩点之间的距离（由用户输入）

-distance 记录到O的最短距离（由程序计算）

第一步：初始化

将O放入U distance设为0 其他顶点全放入U 这些顶点中 如果顶点与O相连 distance设为俩点间的距离 否则 distance全设为无穷大

第二步：更新 从U中选取distance最小的顶点Px放入S 并把所有与Px相连的顶点Px`的distance设为f

这里有一个性质：初始化后的算法运行过程中，已经放入S的顶点的distance不会再变小，即，一旦我们把顶点Px放入S，代表我们已经找到了O->Px的最短路径。 证明：Px的distance就是Px到O的最短距离。

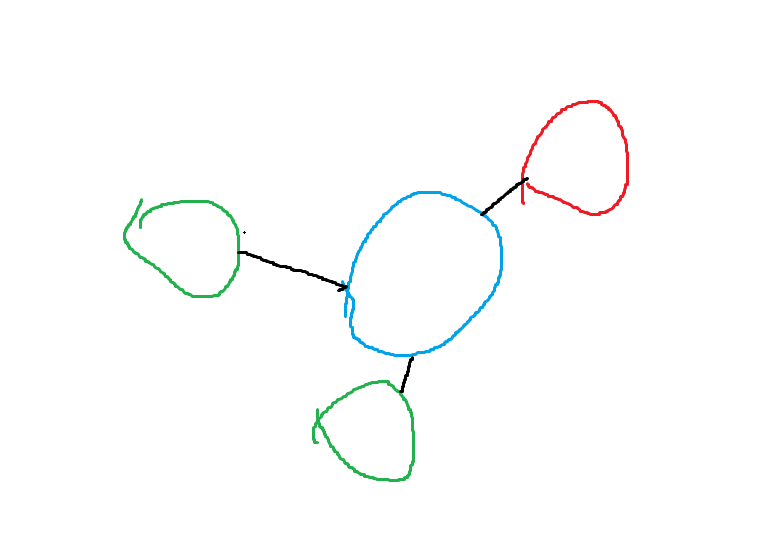
蓝色顶点：Px

绿色顶点：S中与Px相连的顶点

红色顶点：U中与Px相连的顶点

由于，每个绿色顶点都与Px进行过“distance设为f”的运算，所以能保证：如果中间点只有来自S的顶点，Px的distance就是Px到O的最短距离，我们把该路径记作P。 同时，不可能有一条更短的S外的顶点（不含Px）的路径P` ，现在我们来证明这一点： ​ 假设有一条经过S外的顶点（不含Px）的O到Px的最短路径P`，那么一定有顶点y满足：

1.y属于S。

2.y与某S中顶点Ps相连。

3.y不是Px。（再次强调）

4.y在满足以上条件的顶点中distance最小

由操作规程，显然，此刻有y的distance>=Px的distance。

显然P`的长度大于P的长度。

但这只是这一时刻，我们还应该证明，直到算法完成，都有y的distance>=Px的distance。

如果y的distance想要变小，那就必须有另一条路连上他，例如：

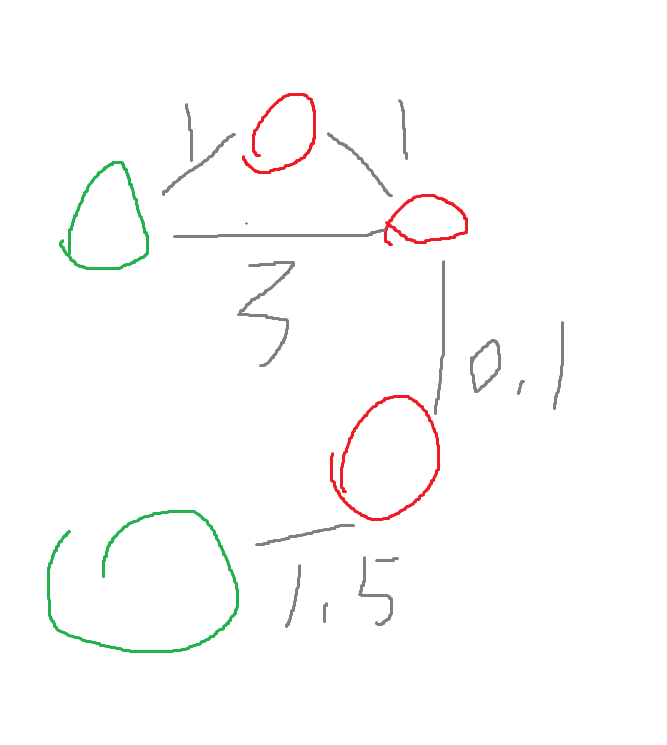
但是，显然，如果distance能靠另一条路变小，他就不满足“4.y在满足以上条件的顶点中distance最小”。

因此，直到算法完成，都有y的distance>=Px的distance。

引入一个更正式的概念：循环不变量

循环不变量是在算法循环的开始、每次迭代后、以及循环结束时都保持为真（成立）的一个条件或性质。

你可以把它想象成算法循环中一个永恒的真理。无论循环执行了多少次，这个真理始终不变。我们通过证明这个真理在循环之初成立，并且每次循环都保持成立，来最终证明算法结束时得到了正确的结果。

那么，我们目前知道了，迪杰斯特拉有俩个关键的循环不变量:

1被选入S的Px的distance就是Px到O的最短距离。

2.迭代过程中，U中Px的distance不会被更新成小于当前S中最大的distance

第三步:重复更新，直到得出结果

显然，在上述原理中，我们只能得到O到F的最短距离，如果要得到路径，只要在计算f的时候，记录提供最小值的父顶点就行。

显然，负权边会导致循环不变量1和2都失效，迪杰斯特拉正确性随之失效。

显然，迪杰斯特拉不能找到所有最短路径。